Groupes ponctuels de symé

Groupes ponctuels de symétrie

Jump to: navigation, search

Voici les tables de caractères des principaux groupes ponctuels de symétrie.

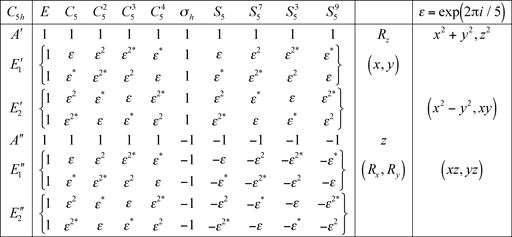
Dans les tables, ε désigne un nombre complexe précisé dans le tableau, et ε^* désigne son conjugué complexe.

Malgré un soucis de relecture et re-relecture, il peut toujours persister une erreur quelque part. Soyez donc attentifs et merci de signaler toute erreur.

Version téléchargeable en PDF : Theorie_des_groupes.pdf (248 ko) (dernière mise à jour du fichier : 21/11/2011)

Sommaire

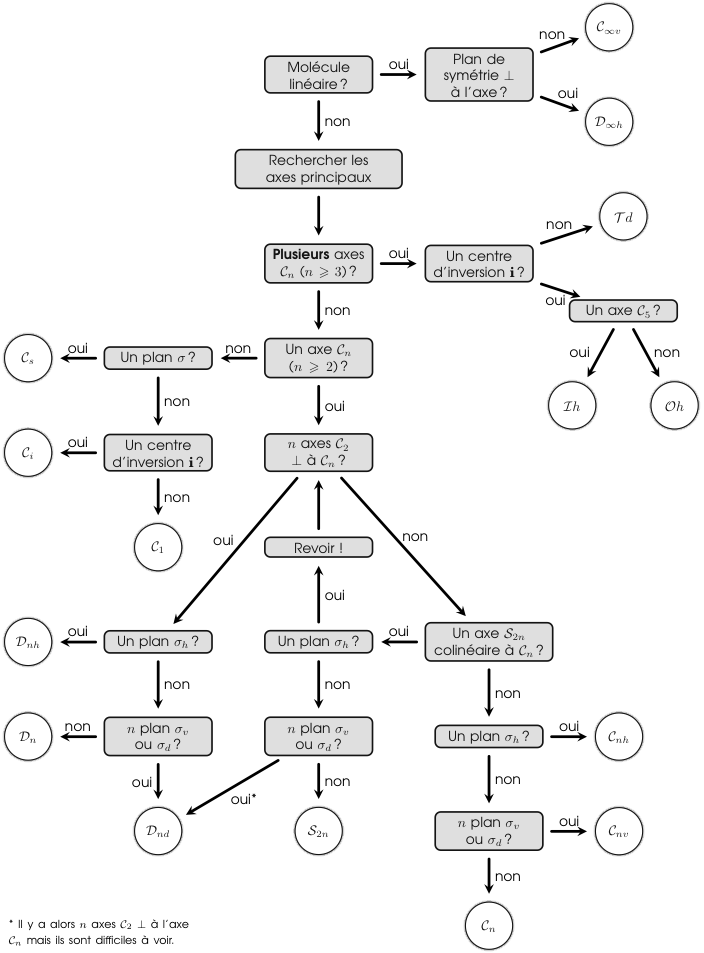
1 Recherche du groupe ponctuel de symétrie d'un objet
2 Groupes non axiaux
3 Groupes Cn
4 Groupes Dn
5 Groupes Cnv
6 Groupes Cnh
7 Groupes Dnh
8 Groupes Dnd
9 Groupes Sn
10 Groupes cubiques
11 Groupes icosaédriques
- 11.1 Groupe I
- 11.2 Groupe Ih
12 Groupes linéaires
13 Groupe de rotation
- 13.1 Groupe K ou R3i
14 Groupes doubles

1 Recherche du groupe ponctuel de symétrie d'un objet

Image:Recherche_groupe_ponctuel.gif

2 Groupes non axiaux

2.1 Groupe C₁

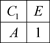
Image:Groupe_C1.gif

2.2 Groupe C_s

Image:Groupe_Cs.gif

2.3 Groupe C_i

Image:Groupe_Ci.gif

3 Groupes C_n

3.1 Groupe C₂

Image:Groupe_C2.gif

3.2 Groupe C₃

Image:Groupe_C3.gif

3.3 Groupe C₄

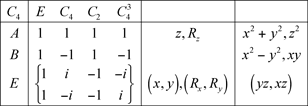
Image:Groupe_C4.gif

3.4 Groupe C₅

Image:Groupe_C5.gif

3.5 Groupe C₆

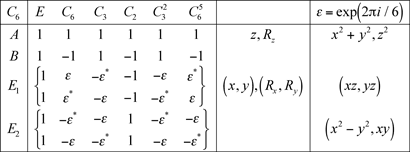
Image:Groupe_C6.gif

3.6 Groupe C₇

Image:Groupe_C7.gif

3.7 Groupe C₈

Image:Groupe_C8.gif

4 Groupes D_n

4.1 Groupe D₂

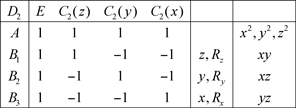
Image:Groupe_D2.gif

4.2 Groupe D₃

Image:Groupe_D3.gif

4.3 Groupe D₄

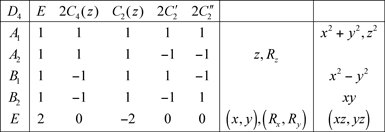
Image:Groupe_D4.gif

4.4 Groupe D₅

Image:Groupe_D5.gif

4.5 Groupe D₆

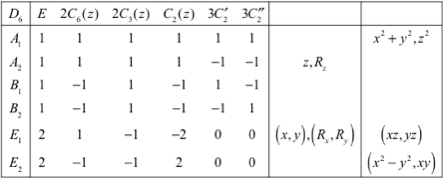
Image:Groupe_D6.gif

5 Groupes C_nv

5.1 Groupe C_2v

Image:Groupe_C2v.gif

5.2 Groupe C_3v

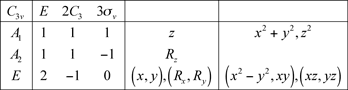
Image:Groupe_C3v.gif

5.3 Groupe C_4v

Image:Groupe_C4v.gif

5.4 Groupe C_5v

Image:Groupe_C5v.gif

5.5 Groupe C_6v

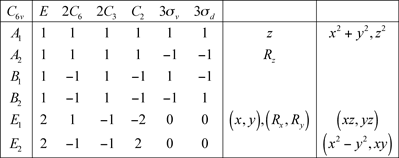
Image:Groupe_C6v.gif

6 Groupes C_nh

6.1 Groupe C_2h

Image:Groupe_C2h.gif

6.2 Groupe C_3h

Image:Groupe_C3h.gif

6.3 Groupe C_4h

Image:Groupe_C4h.gif

6.4 Groupe C_5h

Image:Groupe_C5h.gif

6.5 Groupe C_6h

Image:Groupe_C6h.gif

7 Groupes D_nh

7.1 Groupe D_2h

Image:Groupe_D2h.gif

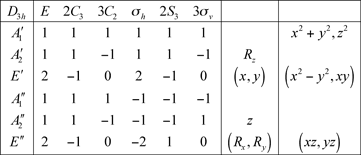
7.2 Groupe D_3h

Image:Groupe_D3h.gif

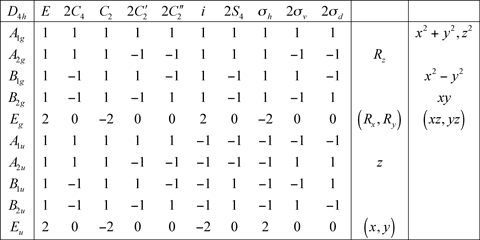
7.3 Groupe D_4h

Image:Groupe_D4h.gif

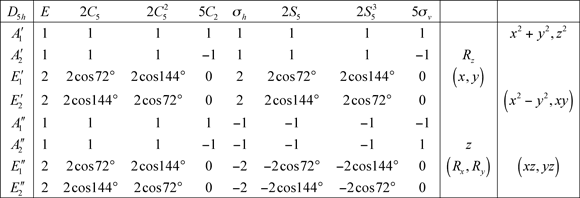
7.4 Groupe D_5h

Image:Groupe_D5h.gif

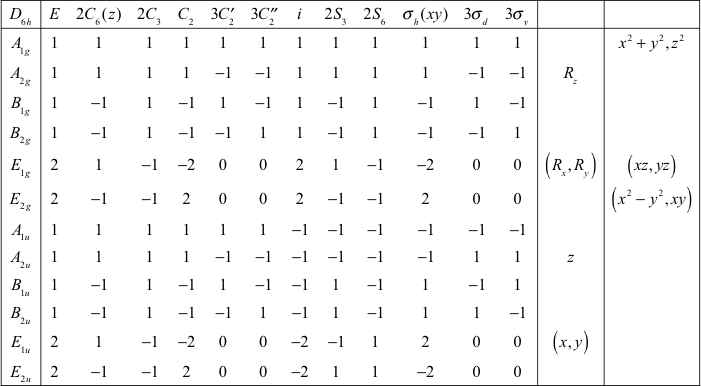
7.5 Groupe D_6h

Image:Groupe_D6h.gif

7.6 Groupe D_8h

Image:Groupe_D8h.gif

8 Groupes D_nd

8.1 Groupe D_2d

Image:Groupe_D2d.gif

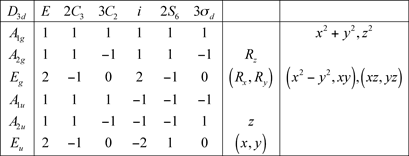
8.2 Groupe D_3d

Image:Groupe_D3d.gif

8.3 Groupe D_4d

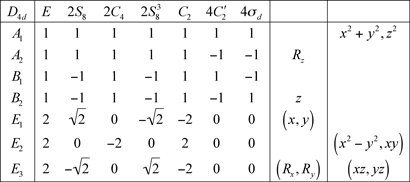
Image:Groupe_D4d.gif

8.4 Groupe D_5d

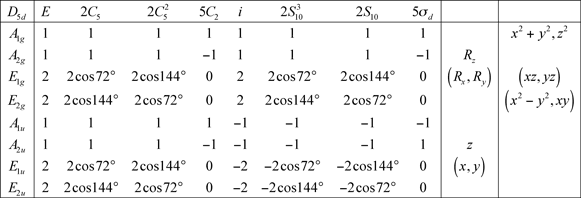
Image:Groupe_D5d.gif

8.5 Groupe D_6d

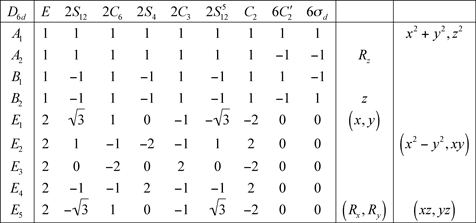
Image:Groupe_D6d.gif

9 Groupes S_n

9.1 Groupe S₄

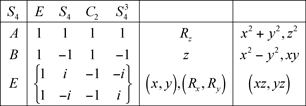
Image:Groupe_S4.gif

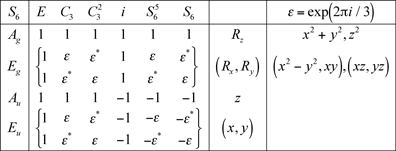
9.2 Groupe S₆

Image:Groupe_S6.gif

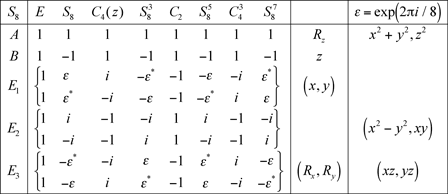
9.3 Groupe S₈

Image:Groupe_S8.gif

10 Groupes cubiques

10.1 Groupe T

Image:Groupe_T.gif

10.2 Groupe T_h

Image:Groupe_Th.gif

10.3 Groupe T_d (tétraédrique)

Image:Groupe_Td.gif

10.4 Groupe O

Image:Groupe_O.gif

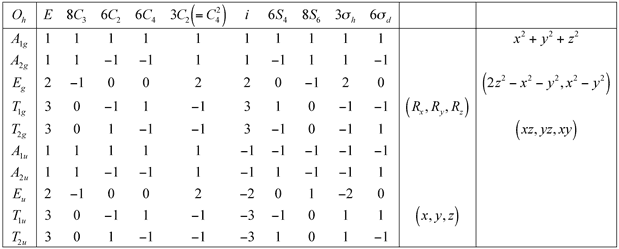
10.5 Groupe O_h (octaédrique)

Image:Groupe_Oh.gif

11 Groupes icosaédriques

11.1 Groupe I

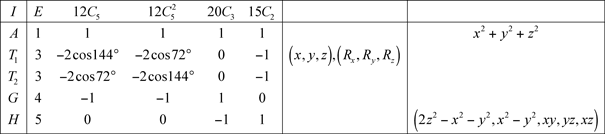
Image:Groupe_I.gif

11.2 Groupe I_h

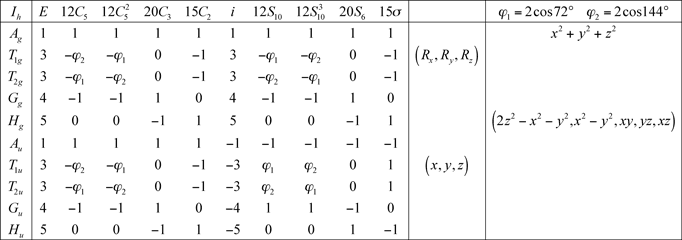
Image:Groupe_Ih.gif

12 Groupes linéaires

12.1 Groupe C_∞v

Image:Groupe_Cinfv.gif

12.2 Groupe D_∞

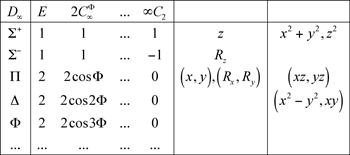
Image:Groupe_Dinf.gif

12.3 Groupe D_∞h

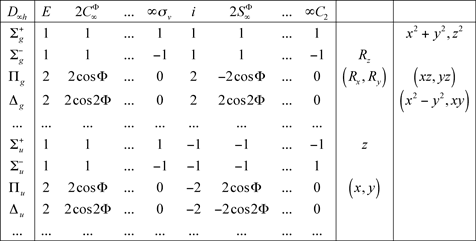
Image:Groupe_Dinfh.gif

13 Groupe de rotation

13.1 Groupe K ou R_3i

Image:Groupe_K.gif

14 Groupes doubles

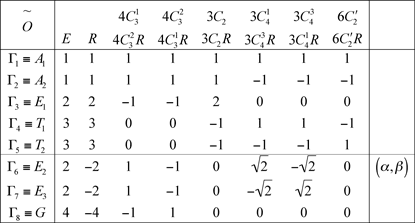
Dans les groupes doubles suivants, R représente l'opération de rotation d'angle 2π. L'opération identité est R².

14.1 Groupe double D₂

Image:Groupe-double_D2.gif

14.2 Groupe double D₃

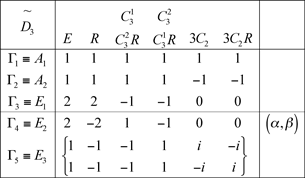
Image:Groupe-double_D3.gif

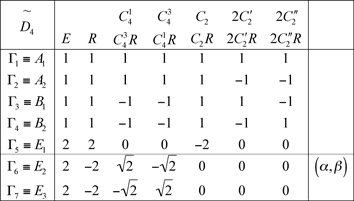
14.3 Groupe double D₄

Image:Groupe-double_D4.gif

14.4 Groupe double Õ

Image:Groupe-double_O.gif