Exercices thermod

T1- Dans un domaine de pressions, l’équation d’état d’un gaz est:
|
|
où B ne dépend que de la température T.
Exprimer le coefficient de dilatation à pression constante  et le coefficient de compressibilité isotherme
et le coefficient de compressibilité isotherme  du gaz.
du gaz.
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )
T2- Un gaz obéit à l'équation de Van der Waals:
|
|
où a et b sont des constantes.
Montrer que
|
|
et que
|
|
T3- Quelle augmentation de pression faut-il exercer sur un liquide ou sur un solide pour supprimer sa dilatation lors d'une élévation de température  T.
T.
|
Application numérique: |
|
|
|
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )
T4- a) exprimer en fonction de  et de
et de  le travail reçu par un système au cours d’une transformation élémentaire réversible en fonction de dP et de dT.
le travail reçu par un système au cours d’une transformation élémentaire réversible en fonction de dP et de dT.
b) examiner le cas particulier du travail reçu lors d’une compression finie et isotherme lorsque  et
et  sont supposés constants (solides ou liquides).
sont supposés constants (solides ou liquides).
T5- Un solide passe d’un état A à un état C:
a) au moyen d’une transformation ABC.
b) au moyen d’une transformation AC caractérisée par P = P0 + a T. Calculer le travail WAC dans les 2 cas en supposant V, 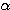 et
et  constants.
constants.
|
|
Un grand ballon fermé par un robinet contient un gaz parfait sous une pression initiale Pi = P0 - h. P0 est la pression
extérieure et h l’indication d’un manomètre à mercure.
On ouvre brusquement le robinet puis on le referme. Le gaz subit alors une compression sensiblement adiabatique et
réversible, suivie d’un refroidissement à volume constant ( la variation de volume du ballon peut être négligée).
A la fin du refroidissement la pression du gaz est devenue: Pf = P0 - h’. Exprimer  = Cp/Cv en fonction de h et de h’.
= Cp/Cv en fonction de h et de h’.
T7- Exprimer la pression en fonction de l’altitude dans l’atmosphère supposée se comportant comme un gaz parfait à
température constante.
La pression au sol étant P0, pression atmosphérique normale , et la température étant de 20°C, calculer l’altitude à laquelle la
pression est réduite à P0/10. On suppose g indépendant de l’altitude, égal à 9,81.
T8- L’atmosphère est maintenant supposée adiabatique, vérifiant la relation:
|
|
Au sol, pression = P0 , température = 20 °C, g = 9,81 m.s-2 et  = 1,4.
= 1,4.
Calculer à quelle altitude la pression vaut P0/10.
T9- Calculer la masse volumique de la vapeur d’eau à 100 °C considérée comme un gaz parfait.
T10- Un litre d’oxygène( O2 = 32 g.mol-1) à 20°C sous 3.105 Pa et 3 litres de dioxyde de carbone (CO2 = 44 g.mol-1) à
50°C sous 2.105 Pa sont mélangés dans un récipient de volume 5 litres à 40 °C. Calculer la pression et la masse molaire du
mélange.
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )

T11- Une masse m d’air ( assimilé à un gaz parfait ) est enfermée dans un cylindre vertical clos par un piston de surface S
qui peut se déplacer sans frottement. La pression atmosphérique PA est supposée constante, on appelle P le poids
du piston.
Dans l’état d’équilibre initial, le gaz occupe un volume V1 sous une pression P1 et se trouve à la température T1 (ambiante). On supposera les chaleurs massiques constantes.
a) trouver l’expression de P1.
b) le cylindre ainsi que le piston sont imperméables à le chaleur. On place sans heurt un poids P' sur le piston.
- décrire et caractériser la transformation qui se produit.
- caractériser l’état final en évaluant la pression P2, la température T2 et le volume V2. Pour simplifier, on posera P2 = n P1.
- examiner le cas particulier où P’ est petit.
- calculer le travail reçu par le gaz pour P' quelconque en fonction de n, P1, V1.
c) à partir de l’état initial (P1, V1, T1) on ajoute progressivement sur le piston de petites surcharges afin de comprimer le gaz jusqu’à la pression finale P3 = P2.
- que peut-on dire de cette transformation?
- quelle est la somme des surcharges?
- caractériser l’état final de la transformation en calculant T3 et V3.
- calculer le travail reçu par le gaz.
d) le cylindre n’est plus supposé imperméable à la chaleur. On opère une compression de P1 à P4 = P2.
- quelles sont les précautions expérimentales pour rendre cette transformation isotherme et réversible?
- calculer le volume final V4.
- calculer la chaleur échangée avec l’extérieur au cours de la transformation.
- représenter graphiquement la transformation dans un diagramme de Clapeyron.
e) on réalise la même transformation en opérant de la façon suivante:
on surcharge le piston avec le poids P’ et dans la transformation rapide qui s’ensuit, on peut admettre l’absence d’échange de chaleur avec l’extérieur, cette phase est suivie d’une autre phase, plus lente, qui mène à l’état final.
- quelles remarques peut-on faire sur cette suite de transformations?
- en faisant l’hypothèse que la transformation passe par l’état considéré en b) , évaluer la chaleur échangée ave l’extérieur.
|
T1 = 300 K |
n = 10 |
V1 = 0,5 L |
|
|
P1 = 1,5.105 Pa |
Cp = 1 kJ.kg-1.K-1 |
T12- Calculer la chaleur nécessaire pour chauffer de 0 °C à 20 °C, de l’air (  = 1,4 ) dont le volume initial est de 50 m3 et la pression initiale de 105 Pa dans les
= 1,4 ) dont le volume initial est de 50 m3 et la pression initiale de 105 Pa dans les
a) V reste constant.
b) P reste constante.
T13- Un récipient de volume 10 litres contient de l’air sous la pression de 80 cm de mercure et à la température de 20 °C.
a) on fait subir à ce gaz une compression isotherme jusqu’à la pression de 800 cm de mercure. Quels sont les échanges de travail et de chaleur avec l’extérieur?
b) on ramène le gaz à sa pression initiale par une détente adiabatique réversible. Quelle est la température finale? Quel est le travail fourni par le gaz?
c) le gaz est enfin ramené à son état initial à pression constante. Quels sont les échanges de chaleur et de travail avec le milieu extérieur?
On assimilera l’air à un gaz parfait de masse volumique 1,293 g.L-1 et de  = 1,4.
= 1,4.
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )
|
|
Exprimer le rendement de ce cycle puis calculez le pour P2 / P1 = 8 et pour P2 / P1 = 20. On donne  = 1,4.
= 1,4.
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )

T15- Un gaz parfait de chaleur molaire Cv = 5/2 R parcourt le cycle réversible ABC.
|
|
On donne PA = 2.105 Pa, TA = 100 K, VA = 3 m3, PB = 4.105 Pa.
a) évaluer les volumes et les températures en B et C.
b) évaluer les travaux sur AB, BC, CA puis sur tout le cycle.
Voir ou télécharger la correction ( par Geneviève GOMI, étudiante )
T16- Une pompe à chaleur quasi-statique fonctionne entre 2 sources constituées par l’eau d’un lac à la température constante t0 = 10 °C et par une masse M d’eau thermiquement isolée. La machine fonctionne dans un sens tel que la masse M d'eau s’échauffe.
a) établir la relation de Clausius:
|
|
au cours d’un nombre entier de cycles de transformations.
b) rappeler la définition de l’efficacité thermique e, et la relier aux températures des 2 sources.
c) au cours d’une transformation infinitésimale, la pompe reçoit le travail  W et fournit la chaleur
W et fournit la chaleur  Q à la source chaude.
Q à la source chaude.
Quelle est la relation entre e,  W et
W et  Q? Exprimer séparément
Q? Exprimer séparément  W et
W et  Q en fonction des températures.
Q en fonction des températures.
d) exprimer le travail W pour une transformation finie qui amène l'eau à la température T.
e) calculer W pour M = 1 tonne quand l’eau a atteint t = 40 °C.
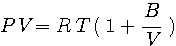








 = 7/5
= 7/5

